Pár hete volt egy Motion oktatásom, ahol ennek a blogbejegyzésnek az ötlete született. A feladat annyi, hogy egy golyót nekilövünk egy csomó kockából álló falnak. Ez látható a következő képen is...
Pár hete volt egy Motion oktatásom, ahol ennek a szimuláció blogbejegyzésnek az ötlete született. A feladat annyi, hogy egy golyót nekilövünk egy csomó kockából álló falnak. Ez látható a következő képen is.
CAD modell készítése
A szimulációhoz a következő testekre van szükségem:
Befogott láncszem:

Kocka:

Láncszem:
 Padló:
Padló:
 Ezt követően ezeket beraktam egy összeállításba:
Ezt követően ezeket beraktam egy összeállításba:
 Az összeállításon belül a padlólap felső felületét a felfüggesztés alsó felületével kényszereztem össze 4 m-es távolságra. Így a golyó közepe a felső síktól (kereken ???? ) 3,732 m-re jön ki.
Szimuláció beállítása
Első lépésben bekapcsoltam a Motion beépülő modult, majd indítottam egy Motion Analysis-t
Az összeállításon belül a padlólap felső felületét a felfüggesztés alsó felületével kényszereztem össze 4 m-es távolságra. Így a golyó közepe a felső síktól (kereken ???? ) 3,732 m-re jön ki.
Szimuláció beállítása
Első lépésben bekapcsoltam a Motion beépülő modult, majd indítottam egy Motion Analysis-t
 Ezek után kontaktokat állítottam:
Ezek után kontaktokat állítottam:
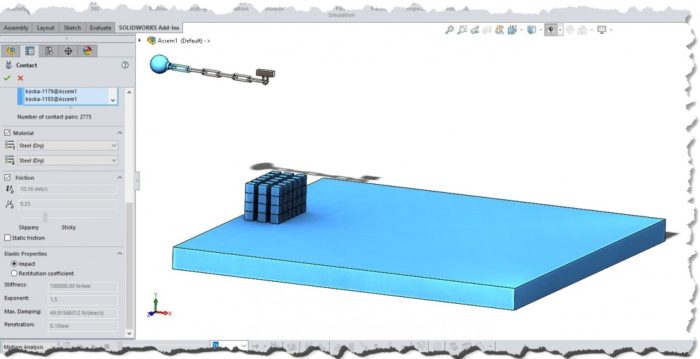 A képen minden ami kék, az ütközhet egymással, az összes többi elemet (lánc és a felfogás) az összeállításon belüli kényszereik tartják egyben. Majd beállítottam a gravitációt ami, lefelé hat (-Y irány a globális koordinátarendszerben).
A megoldónál 25 FPS-t állítottam be számolási gyakoriságnak elindítottam a számolást.
Szimuláció eredménye
A képen minden ami kék, az ütközhet egymással, az összes többi elemet (lánc és a felfogás) az összeállításon belüli kényszereik tartják egyben. Majd beállítottam a gravitációt ami, lefelé hat (-Y irány a globális koordinátarendszerben).
A megoldónál 25 FPS-t állítottam be számolási gyakoriságnak elindítottam a számolást.
Szimuláció eredménye
 CAD modell módosítása
Az előző videóval az volt a bajom, hogy nem repültek a kockák tök messzire, csak kb. a talaj 1/3-áig. Így módosítani akartam valami. Ez a valami a
geometria 1, hosszabb lánc, nagyobb út így több ideje lenne gyorsulni a golyónak,
geometria 2, kisebb tömegű kockáknak nekiütköztetni a golyót,
ütközési számot módosítom (http://help.solidworks.com/2018/english/solidworks/motionstudies/hidd_dve_sim_3dcontact.htmhttps://en.wikipedia.org/wiki/Coefficient_of_restitutionhttp://metal.elte.hu/~phexp/doc/prd/c2s4.htm).
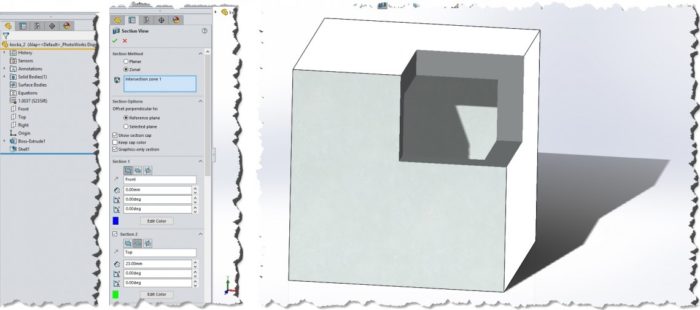
Ezekből az opciókból a másodikat választottam, és a kockára ráraktam egy Héj (Shell) műveletet.
CAD modell módosítása
Az előző videóval az volt a bajom, hogy nem repültek a kockák tök messzire, csak kb. a talaj 1/3-áig. Így módosítani akartam valami. Ez a valami a
geometria 1, hosszabb lánc, nagyobb út így több ideje lenne gyorsulni a golyónak,
geometria 2, kisebb tömegű kockáknak nekiütköztetni a golyót,
ütközési számot módosítom (http://help.solidworks.com/2018/english/solidworks/motionstudies/hidd_dve_sim_3dcontact.htmhttps://en.wikipedia.org/wiki/Coefficient_of_restitutionhttp://metal.elte.hu/~phexp/doc/prd/c2s4.htm).
Ezekből az opciókból a másodikat választottam, és a kockára ráraktam egy Héj (Shell) műveletet.
 Eredmények a módosított geometriával
Eredmények a módosított geometriával
 Sebesség Plotok
A SW Motion a célgéptervezéshez egy dinamikai modul, így ennek az animációnak elkészítéséhez minden időpillanatban elvégzi a mozgáshoz szükséges dinamikai számolásokat, így tartalmaz lekérdezhető számszerű értékeket a grafikus „mi merre megy és milyen útvonalon” adatokon kívül.
Ezek a lekérdezések a szoftveren belül négy kategóriába sorolhatók,
elmozdulás/sebesség/gyorsulás,
erő,
impulzus/energia/teljesítmény,
egyéb mennyiségek.
Sebesség Plotok
A SW Motion a célgéptervezéshez egy dinamikai modul, így ennek az animációnak elkészítéséhez minden időpillanatban elvégzi a mozgáshoz szükséges dinamikai számolásokat, így tartalmaz lekérdezhető számszerű értékeket a grafikus „mi merre megy és milyen útvonalon” adatokon kívül.
Ezek a lekérdezések a szoftveren belül négy kategóriába sorolhatók,
elmozdulás/sebesség/gyorsulás,
erő,
impulzus/energia/teljesítmény,
egyéb mennyiségek.
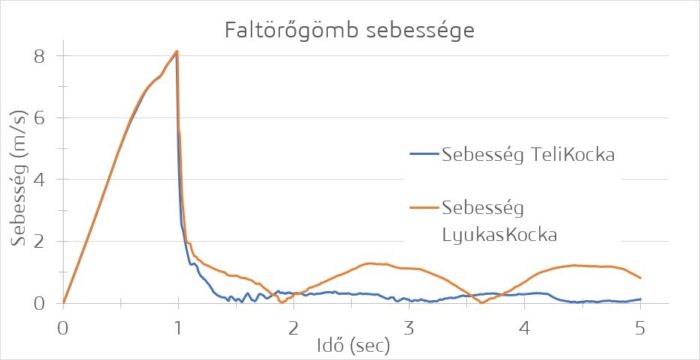
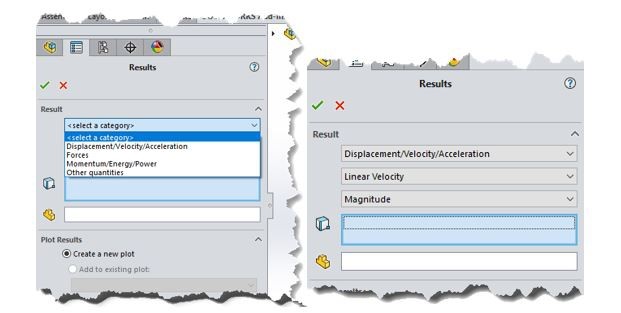 Ezekből a lineáris sebességet és a nagyságot [ Magnitude nagyság=gyök(x irányú sebesség^2 + y irányú sebesség^2+ z irányú sebesség^2)] kiválasztva a következő diagramot állíthatjuk elő a két vizsgált esetre:
Ezekből a lineáris sebességet és a nagyságot [ Magnitude nagyság=gyök(x irányú sebesség^2 + y irányú sebesség^2+ z irányú sebesség^2)] kiválasztva a következő diagramot állíthatjuk elő a két vizsgált esetre: