A mai blogbejegyzésünkben a szülőknek szeretnénk segíteni, akik gyermekük iskolai feladatát szeretnék leellenőrizni és rendelkeznek SOLIDWORKS Premium vagy SOLIDWORKS Simulation Standard csomaggal.
SOLIDWORKS Motion a leckék megoldásának szolgálatában. A mai blogbejegyzésünkben a szülőknek szeretnénk segíteni, akik gyermekük iskolai feladatát szeretnék leellenőrizni és rendelkeznek SOLIDWORKS Premium vagy SOLIDWORKS Simulation Standard csomaggal.
Feladat
A képen látható m tömegű anyagi pontot (kődarabot) eldobom. A dobás szöge 20° a vízszinteshez képest, a kődarab középpontja 11 méterre van a földszinttől. A kezdeti sebesség 15 m/s. A gravitációs gyorsulás g=9,80665* m/s2 és nincs légellenállás!
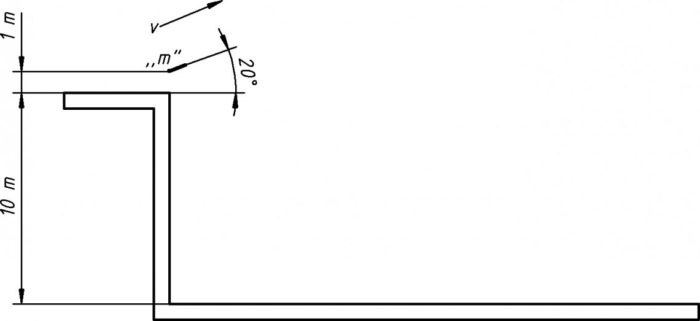Mikor és hol van a legmagasabban? Mikor és hol fog becsapódni?
Analitikus megoldás
Ismert paraméterek
A vízszintes és a függőleges sebességkomponensek értékei:
A gyorsulás vektora:
Nevezzük el a kiinduló pontot A-nak, a dobási út legmagasabb pontját B-nek, és a becsapódás helyét C-nek.
Azt tudjuk, hogy a -g, a vy ellen hat, így a B pontban vy=0 m/s sebességű lesz. Mivel nincs közegellenállás, így vx változatlan. Ezek függvényében felírhatók
Az idő ismeretében kiszámítható az A-B pont közötti magasságkülönbség a négyzetes úttörvénnyel:
Vezessük be azt, hogy C1=v és C2=s0. Így visszakaptuk a középiskolában tanult képletünket:
Vegyük fel úgy a koordinátarendszerünket, hogy az A pontban van. Így az egyenlet végéről az s0=0 m, és a következőképpen néz ki az egyenletünk:
B pont teljes magassága a 0 m-es magassághoz viszonyítva,
B pont sebességvektora:
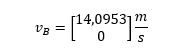A sebességvektorból látható, hogy vy=0 m/s. A becsapódáshoz szükséges idő ezek után számolható a négyzetes úttörvénnyel:
Hagyjuk el az előjelet g elől és rendezzük át az egyenletet:
Az eldobástól a becsapódásig eltelt idő:
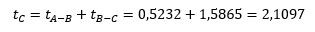Az idő segítségével kiszámítható a becsapódás helye is:
Numerikus megoldás SOLIDWORKS Motion segítségével
Első lépésnek megrajzoltam egy „kődarabot” és a „dombot” amiről ledobtam.
Majd elkészítettem az összeállítást.
Ezek után az első kérdés (milyen magasan volt a legmagasabb pont a test által megtett pályán) megválaszolására, készítettem egy szenzort. Az eredményt nem csak a szenzorból olvastam ki, hanem az y irányú elmozdulás plotját kimentettem CSV-be, amit utána Excelben kiértékeltem.
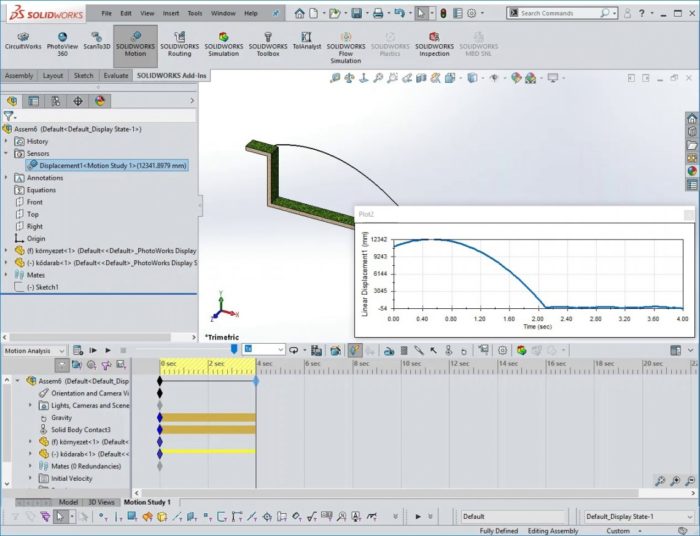
Videó: Legmagasabb pont meghatározása
A szimulációban sB-re 12,3418979 m jött ki, az analitikus megoldásban sB=12,34194654 m. A két érték közötti különbség oka, hogy a SOLIDWORKS Motionben testtel számoltam és nem „m” tömegű anyagi ponttal. Így az általam kijelölt pont a Z tengelye körül el tudott fordulni és ez okozza a 0,048644 mm-es különbséget. Ezek után nem akartam az Exceles adathalmazomat elemezni vagy a SOLIDWORKS Motion diagramját nagyítgatni ahhoz, hogy meghatározzam a becsapódás idejét, így készítettem egy Proximity szenzort. A közelségérzékelőnek 50 m-es hosszt adtam meg, és a 0 méteres magasságra raktam le a „domb” tövébe. Ezek után átléptem esemény alapú mozgástani szimulációra és beállítottam, hogy ha a szenzor jelez, akkor állítsa le a szimulációt. A pontosabb eredmények miatt, a számolás gyakoriságát 250 FPS-re állítottam, azaz ha egyenletes eloszlással számolok, akkor 0,004 másodpercenként számol egyet.
Videó: Becsapódás helye és ideje
A videóban az összidő 2,11 másodperc. Több tizedesjegyre elvégezve a lekérdezést, 2,10675808966939 másodperccel a dobás után állt le a szimuláció. A kézi számolás időszükséglete 2,109668659 másodperc volt. A két érték közötti különbség 0,00291057 másodperc. Az eltérés indokának most is ugyanazt gondolom, mint előbb (szilárdtest vs. anyagi pont), illetve azt, hogy a közelségérzékelő az egész szilárdtestet nézte és nem csak a rajta kijelölt pontot. Ezek után vagy készítek egy újabb szenzort vagy kijelölök az utolsó lekérdezésben egy koordinátarendszert ahhoz, hogy megkapjam sCx-et, azaz az x irányú elmozdulást. Vagy lustaság fél egészség, leolvasom a tengely két végét és kivonom egymásból, az abszolút értéküket.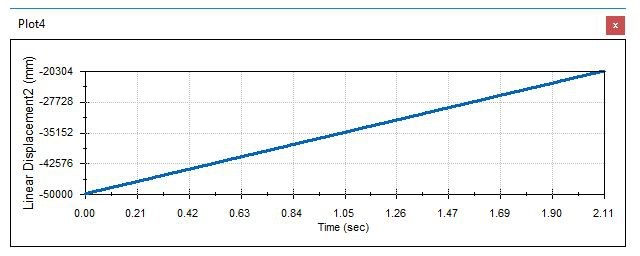
Ha ezt választom, akkor az x irányú elmozdulás:
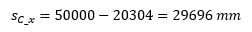Ha pontosabb eredményre van szükségem, akkor 5 tizedesjegy pontosságra a következőt kapom:
A számolt érték 29,73660107 m. A két érték különbsége 0,041025211 m, ami az analitikus érték 0,14%-a.