A mai blogbejegyzésünkben szeretnénk újra segítséget nyújtani a szülőknek, akik gyermekük iskolai mechanika feladatát szeretnék leellenőrizni és rendelkeznek SOLIDWORKS Premium vagy SOLIDWORKS Simulation Standard csomaggal.
Mechanika feladat statikai része
Feladat: Rajzolja meg az igénybevételi ábrákat a képen látható tartóhoz, majd számolja ki a rúd közepén ébredő feszültséget.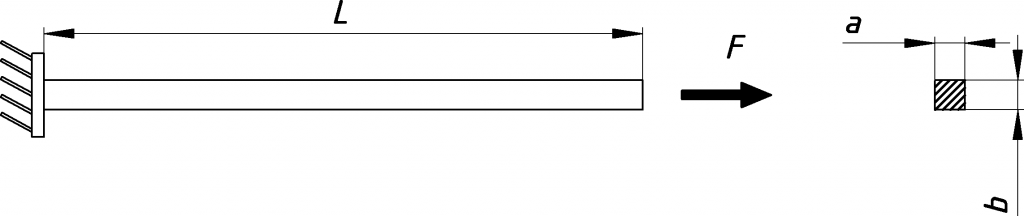
Adatok:
l= 1000 mm
a=b= 50 mm
F= 100 kN
Feltételezzünk a falban egy erőt, ami vízszintes és ellenkező irányba hat mint az F erő. Így felírható a következő összefüggés:
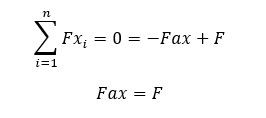Ezek segítségével megrajzolhatók az igénybevételi ábrák:
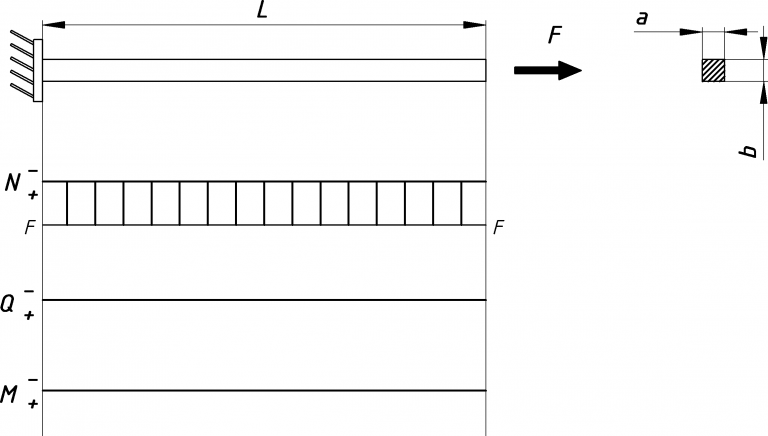Szilárdságtan
Tudjuk, hogy a mechanika feladatban szeplő tartó teljes hosszán F erő, azaz 100 kN normál irányú erő ébred, így a rúd közepén is 100 kN a terhelés.
Írjuk fel húzófeszültség kiszámításához a következő képletet: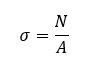
A képletben N a normál erő, A a keresztmetszet. A normál erőt már tudjuk, ezt számoltuk ki előbb, a keresztmetszet csak az ismeretlen. Az egyik lehetőség, hogy kiszámoljuk, a másik, hogy kiszámoltatjuk a SOLIDWORKS-szel.
Amennyiben számolunk, akkor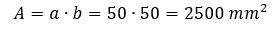
Amennyiben le szeretnénk mérni, ahhoz a Metszetjellemzők (Section Properties) parancsot kell használnunk.
A keresztmetszet mérése a következő videón látható:
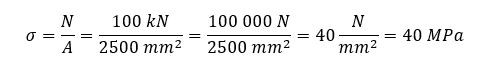
Az igénybevételi ábrák alapján a normál erő konstans a rúd mentén, így a rúd teljes hosszán 40 MPa feszültség ébred.
Ugyanez a mechanika házi feladat SOLIDWORKS Simulationben
CAD geometria Első lépés a geometria megrajzolása. A videóban az látható, hogy húzok egy vonalat, aminek a hossza 1m, ezt átváltja a SW 1000 mm-re (mm az alapmértékegységem), ezek után középsíkhoz kihúzom, és a vonal vastagságát is a középsíkhoz adom meg.VEM rúdmodell Következő lépés a SOLIDWORKS Simulation moduljának a betöltése.
A videóban az látható, hogy a CAD geometriát szilárdtestként rajzoltam meg (és nem a Hegesztés (Weldments) modullal acélszerkezetként), így rúdmodellé alakítom a testet, majd hozzáadok egy S235JR anyagot. Ezek után a test egyik felét „befalazom” a másikat meg megterhelem az F erővel.Futtatás és kiértékelés Ezek után rákattintok a futtatás parancsra, majd a feszültségeket és az erőket. A futtatás után megkapjuk a feszültség, elmozdulás és biztonsági tényező plotokat. Az alapértelmezett feszültség plot a hajlító és a húzó erőből számolt σ feszültségek. Jelen erőrendszerben csak húzás van, így létrehoztam egy új feszültség plotot, ami csak a húzást mutatja, majd az Axiális (normál irányú) igénybevételi ábrát ábrázoltam.
Ezek után kilistáztam a megfogásban ébredő reakcióerőt és a rúdban ébredő erőt (végeselemes háló) elemenként.VEM szilárdtest Ezt követően az 1 dimenziós rúdmodellem szimulációját átmásoltam egy Study 2 nevű szimulációba és átállítottam szilárdtestre a modellt. Ezek után a megfogást és az erőt újra kellett definiálnom (mert a rúdmodellnél csak egy vonalam volt és annak a végeit választottam ki a kényszereknek, itt viszont felületeim vannak). Ezek után rákattintottam a futtatásra és az automatikusan generált hálóval lefuttattam a szimulációt. Az eredményeket összehasonlítva a rúdmodellel, a maximum és a minimum értétkek eltérnek egymástól. Ez a következő videón látható.
A rúdra állandó feszültséget várnék, és a rúd eleje (szemre kb. 100-150 mm) nem konstans színű, ezért sűríteni szeretném a hálót. Ezt globálisan és lokálisan is megtehetem. A videókon valós futtatási idő látható, így nem érzem fontosnak, hogy számolási időt spóroljak a lokális sűrítéssel, így globálisan sűrítek. (Ez a következő videón látható.) Ezek után leellenőriztem a reakcióerőket.VEM felületmodell
Eddig láttuk a szimulációt 1 és 3 dimenziós modellel, így a teljesség kedvéért elkészítem felületmodellel is, azaz 2D-ben. Az előző esetben a rúdmodell egy vonal volt és azt osztotta fel véges elemre és azokkal számolt a szoftver, a szilárdtest egy térbeli test, amit tetraéderekre osztott fel a szoftver. Jelen esetben a felületmodellnek nincs vastagsága, így ez egy héj, aminek a vastagságát nem hálózza a szoftver, így háromszögekből építi fel a végeselemes modellt. Összegzésül a mechanika feladat megoldásához
Ez egy rúd/gerenda modell, ami vonal (egy dimenziós elem), se vastagsága se szélessége nincs és a szoftver ezt darabolja véges (vonal) elemre.
Ez egy felületmodell, térbeli kiterjedése van, de a hálózása csak „síkban” történik, azaz a vastagságot nem hálózza a szoftver. Az egész testet véges számú háromszög elemre bontja fel a szoftver. 
Ez egy szilárdtest, aminek van térbeli kiterjedése és vastagsága is. A hálózó ezt a típusú testet véges számú tetraéderből építi fel.
A felvezetés után nézzük a Simulation-ön belül felületmodell létrehozásának menetét.
A következő videóban átmásolom az eddigi beállításaimat egy következő szimulációs tanulmányba, majd a Simulation-be beépített felület létrehozása paranccsal felületmodellt készítettem a szilárdtestből. Ezek után beállítottam felületmodell vastagságát.
Ezek után azokat a befalazást és az erőt amik eddig felületekre hivatkoztak átállítottam élekre (mert a felületek már nem léteznek az egyszerűsítés miatt), majd behálóztam a modellt.
Ezt követően lefuttattam a szimulációt és pár ponton megnéztem a feszültségértékeket, amik a várt 40 MPa értékűek.
A belső felületmodell készítő parancson kívül a felületmodellezést a Felület (Surface) eszköztárral is el lehet végezni. A következő videóban ennek a lépései láthatók. A videóban első lépésnek készítettem egy új konfigurációt a felületmodellnek. Ezek után (lustaság fél egészség szerint), nem újra megrajzoltam a testet, hanem leloptam a közép sík felületét a Középfelület (Mid-Surface) paranccsal, majd kitöröltem a meglévő szilárdtestet.
Az eszköztárban nem Középfelület nincs kirakva alapból, így aki ezt a parancsot szeretné használni, annak javaslom, hogy keresse meg a Parancs keresővel.
FYI: új parancsokat a Parancs keresőből Drag&Drop-pal ki lehet rakni a szalagmenükre.
Eredmények összehasonlítása
A következő videóban a három szimuláció elmozdulásértékei láthatók.
Amennyiben ez az érték analitikusa kellene nekem, azt a következő képlettel tudom kiszámolni:
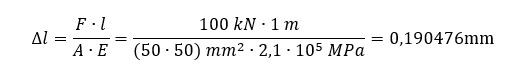
* és a kiszámolásához (számológépbe bepötyögés + papírra leíráshoz) szükséges idő.
Hetyei Csaba