Az előző részekben a modell építési stratégiákkal, ökölszabályokkal ismerkedhettünk meg. Láttuk hogy sokféleképpen megközelíthetünk egy feladatot, ami nyilván kihatással lesz arra, milyen ábrát fogunk kapni eredményül. Nagyon fontos, hogy eredményeket kapunk és nem végeredményt! A végeredmény mérnöki tudás alapján levont következtetésünk lesz az ábrák alapján. Ez logikus, hiszen a számítógép csak azt a feladatot ismeri, amit mi definiáltunk neki. Illetve a modellekben nem számoltunk minden részlettel. Ezek nem csak az egyszerűsítésekből adódnak. Nem tudunk mindent figyelembe venni, ezek közt lehetnek fontos és kevésbé fontos tényezők. Az alkatrész színe például nem igazán fogja befolyásolni, hogyan bírja a terhelést. A felület érdessége viszont lehet, mégsem fogjuk amiatt rücskösre készíteni a CAD modellt. Szakmai belátásunk szerint viszont figyelembe vehetjük egy biztonsági tényezővel.
HÁLÓZÁS ÉS MEGOLDÓ
Idáig viszont el kell jutni, amihez a hálózáson és a megoldón keresztül vezet az út. A peremfeltételek definiálásával, illetve azzal, amit idáig tárgyaltunk, matematikai modellt építettünk.Ezt kell megoldhatóvá tenni a számítógép számára, erre való a hálózás. Azután beszélhetünk VEM-ről (Véges Elem Modell), miután sikeresen behálóztuk a testeket. Itt látszólag nem történik nagy dolog, ám azt fontos megérteni, hogy a matematikai modell a gondolatainkat, megközelítésünket tartalmazza, ám a hálóval válik számtanilag kezelhetővé, mondhatni ezáltal válik láthatóvá, vagy értelmezhetővé a gép számára. A láthatóság olyan szempontból jó hasonlat, hogy mint egy filmnél itt is számít, milyen felbontásban nézzük. A számítógép jellemzően az ócska minőséget kedveli velünk ellentétben, de létezik kompromisszum.
Szerencsére a Solidworks Simulation itt is segít nekünk, hogy könnyedén és megfelelő hálót készítsünk. Rengeteg típusú létezik, négyszög, háromszög, hexagon stb. és ezek keveréke. Hogy ne kelljen választanunk közölük a Solidworks Simulation háromszög alapúakkal dolgozik. Ennek az az oka, hogy ez a legszéleskörűbben használható fajta. Mondhatjuk, hogy bármit be lehet vele hálózni és nem is kíván különösebb szakértelmet, ellentétben más említett típusokkal, amelyek nem használhatók minden geometriára, és építésük is időigényesebb.
Nézzük meg részletesebben, milyen hálókkal van lehetőségünk dolgozni.
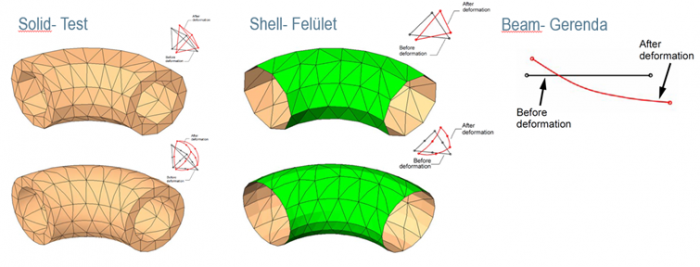
felületháló - shell- használata
A test, azaz Solid háló elemeit tetraéderek alkotják, tehát olyan térelemek, amelyeknek minden oldala háromszög. Ez a típus általános formájú testek hálózására alkalmas, melyek méretei a tér különböző irányaiban kb. azonos nagyságrendűek. Természetesen testhálóval bármit be lehet hálózni, de nem biztos, hogy megéri. Jelentősen csökkenthetjük a számítási időt, és közben pontosság rovására sem válik feltétlenül, ha shell, azaz felülethálót használunk. Az előbbiek alapján gondolhatjuk, hogy ez olyan testeknél lesz hasznos, amelyek egyik dimenziója jóval kisebb, mint a többi ezt egyben vehetjük alkalmazási feltételnek is. Erre tipikus példa a lemez, illetve abból hajtott alkatrészek, hogy erre ne kelljen külön gondolnunk a Solidworks Simulation Sheetmetallal, valamint Surface-szel készített alkatrészeket alapértelmezetten így hálóz. Lemezalkatrészeknél még az anyagvastagságot is automatikusan hozzárendeli, 0-vastagságú felületnél ezt értelemszerűen nekünk kell megadni. A harmadik típus a Beam vagyis Gerenda háló, ez a Weldment-tel készített alkatrészek alapértelmezett hálója, jelentős egyszerűsítés amikor ilyen hálót használunk, cserébe villámgyorsan fut, leginkább sok elemből álló hegesztett szerkezeteknél érdemes használni őket. Az alapértelmezett típusok nem jelentik azt, hogy nincs más mód behálózni a testeket. Ha úgy gondoljuk, hogy másik hálótípus jobban megfelel a célnak, vagy pontosabb eredményt ad, van átjárási lehetőségünk. Én ennél a példánál ezt nem állítottam. A dobozt, amelyben a készülék van lemezből készítettem és ennek megfelelően lett hálózva is. A többi elem testhálót kapott.
A háló készítés egyik legnagyobb kihívása, hogy a különböző nagyon eltérő méretű geometriákat és testeket hogyan tudjuk behálózni. Ennek nagy részét megoldhatjuk egyszerűsítésekkel, de nem mindent. Talán az egyik leggyakoribb kihívás hálókészítéssel kapcsolatban ez. Ennek érdekében 2021-ben a Solidworks Simulation bevezette, hogy alapértelmezett legyen az inkompatibilis hálózás.
Inkompatibilis hálózás
Mi az oka? Mit jelent ez? Egyrészről nagy könnyítés a felhasználónak, mert ilyen hálót sokkal könnyebb készíteni mint kompatibilis társát. Ennek oka az, hogy külön hálót készít testenként, amiket összekapcsol, így nem kell összehegeszteni az elemeket, mint egy kompatibilis hálónál. Kompatibilis háló készítésére is van lehetőség, eredetileg ez a módszer pontosabb, illetve futtatni is könnyebb, ám a továbbfejlesztett algoritmusoknak köszönhetően mára nem számottevő a különbség. Én is az alapértelmezett beállításokat használom és azt tapasztalom, hogy sokkal kevesebbet kell hálókészítéssel bajlódnom, és az eredmények is megfelelőek.
Aki jobban megnézte az előző ábrát észrevehette, hogy nem teljes a leírás a hálótípusokkal kapcsolatban. Felső és alsó sort is találunk, itt valóban érdemes megkülönböztetést tenni. Láthatjuk, hogy a felső sor szögletesebb, de ami ennél is többet árul el az az ábrák jobb felső sarkában található magyarázó ábra, ami a kiindulási és deformált állapotot kívánja szemléltetni. Ez alapján megkülönböztetünk high és low quality mesh-t. Érthető az elnevezés, hiszen már az ábrán is látszódik, hogy az alsó sor sokkal szebben leköveti a geometriát, nyilván ez a high quality mesh. Ám mint azt már sejthetjük, nincs előny hátrány nélkül. Itt sincs ez másképp a high quality elemek nem csak a csúcsokban tartalmaznak csomópontot, hanem az oldalfelezőkben is. Ezáltal azoknak a csomópontoknak az elmozdulásával is kell számolni ami hosszabb futási időt eredményez.
Eddigiek alapján megfigyelhettük a következő összefüggést, amelyet ökölszabálynak is tekinthetünk:
Ha egy tényező növekszik akkor a másik kettőnek is kell. Ezt mindig célszerű szem előtt tartani.
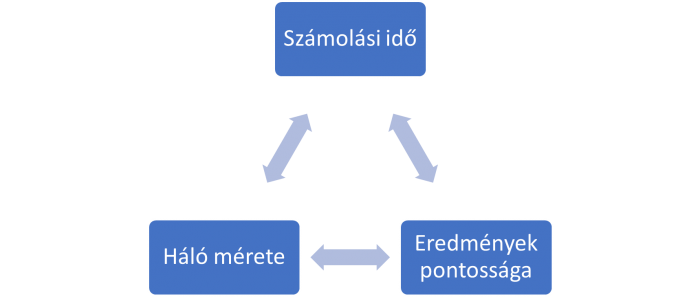
Most, hogy ezt megállapítottuk térjünk rá a példára, mit és hogyan érdemes hálózni. Arra nem térek ki részletesen, hogy a különböző megközelítések, finomítások során milyen hálót használtam. A gyors futtatás érdekében, gyér hálót alkalmaztam az eredmények jellege volt csak érdekes számomra nem maguk a számok.
A végső eredményeknél azonban eltértem az alapbeállításoktól és kiegészítettem azokat. A maximális és minimális hálóméreteket átírtam, valamint lokális sűrítést is alkalmaztam:
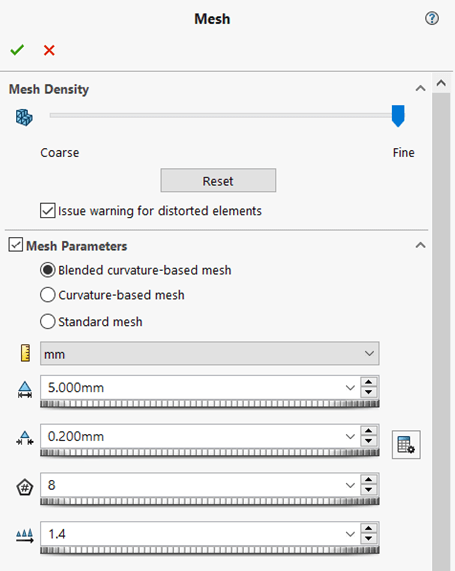
Beírtam a paramétereket egy a modell méreteihez igazodó tartományba, illetve kedvenc hálózó algoritmusomat alkalmaztam a Blended curvature-based típust. Alapvetően bármelyik jó, amelyik behálózza a modellt. A Standard szögletesebb geometriáknál előnyösebb, a Curvature-based pedig ívesebb testeknél. Blended társuk egy picivel lassabb náluk, de cserébe szebb strukturáltabb hálót ad vegyes geometriáknál. Nem mellesleg, bár itt nem lett volna rá szükséges, az akadályokat is ez veszi a legkönnyebben.
Az alap háló beállítás nem feltétlenül elég minden hely alapos elemzésére, így a kényesebb/ érdekesebb helyekre hálósűrítést alkalmaztam:
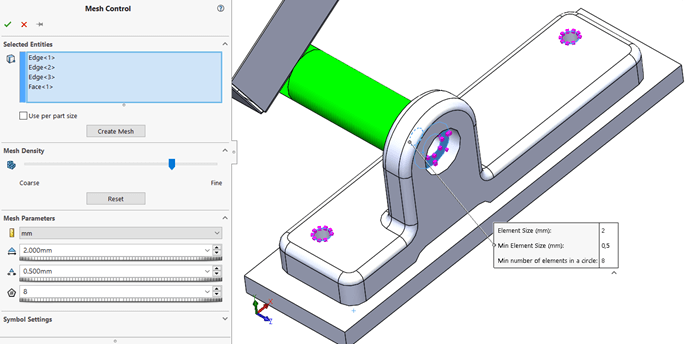
Ennek végeredménye az alábbi háló:
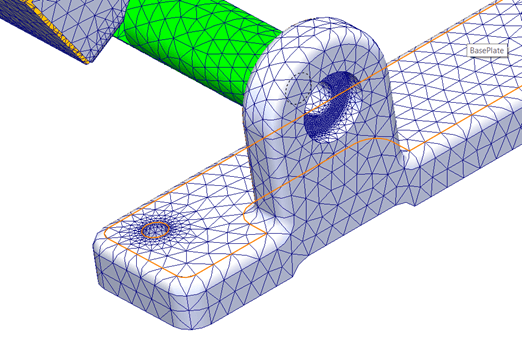
Ezzel a kompromisszummal nem növeljük feleslegesen a futási időt, de ahol szeretnénk pontosabb eredményt kapni ott lehetőségünk van rá.
VEM - véges elem modell- vizsgálat
Definiáltuk a feladatot, be is hálóztuk, létrehoztunk egy igazi VEM-et, melyet futtathatunk. De hogyan? Ez általában számunkra a legegyszerűbb rész nem úgy mint a gépnek. A felállás olyan, mint mikor tanárunk kiadta a házi feladatot. Neki egyszerű volt, mert csak lediktálta vagy felírta az egyenleteket, mi meg dolgozhattunk vele jó sokat. Szerencsére „diákunk” nagyon jó, vagy legalábbis sokkal gyorsabb az ilyen feladatok megoldásában. A néhány tízezertől több millió egyenletet, amit kiosztunk neki egy kattintással, hozzánk képest nagyságrendekkel gyorsabban oldja meg. Persze nem mindegy mekkora a feladat és milyenek a számítógépünk képességei. Ezektől függően a megoldási idő, néhány perctől néhány napig is eltarthat. Annyit érdemes tudni ezzel kapcsolatban, hogy az erőforrások szempontjából elsősorban a CPU, majd a RAM ami befolyásolja a futtatási időt.

MEGOLDÓ
Érdemes néhány szót ejteni a megoldóról is, hiszen rá hárul a feladat oroszlán része. A Study Propertiesben részletesebb beállításokat végezhetünk a futtatásra vonatkozóan, itt állíthatjuk a megoldó típusát is. Alapvetően kétfajta típus közt választhatunk Direkt és Iteratív megoldók közt. Kezdetben érdemes Direkt megoldót használni, mivel pontosabb és szélesebb körben alkalmazható. Hátránya viszont, hogy sokkal erőforrás igényesebb. Így nagy méretű modellekhez inkább iteratív megoldót használata javasolt vagy az erre a célra fejlesztett Direkt megoldót.
De milyen feladat számít nagynak? Fontos tudni, hogy a szimulációs modellek méretét, nem mm-ben mérjük, hanem a háló csomópontjainak, illetve azok szabadságfokainak számában.
Jelen példánk nem számít nagy modellnek, így Direkt megoldót választottam hozzá. Ám ezzel nem kell foglalkoznunk, ha alapértelmezett beállításként ezt választjuk ki. A SOLIDWORKS Simulation jelzi, ha a probléma mérete megköveteli másik megoldó használatát.
De mivel is dolgozik, ténylegesen mit számol a megoldó? Ehhez érdemes megnéznünk a szimuláció alapegyenletét mely nem annyira bonyolult, mint amilyennek elsőre látszik.
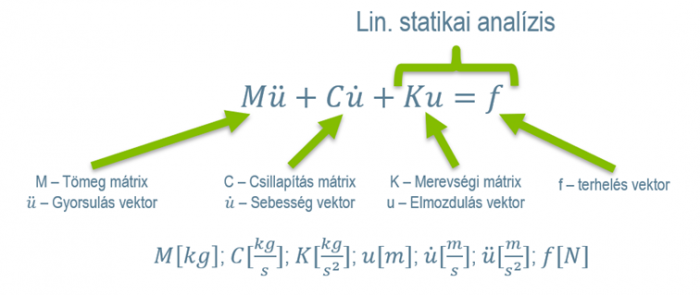
Ahogy látjuk, a lineáris statika ennek az egyenletnek csak egy kis részét képezi, ami nagyban egyszerűsíti a megoldást ám a gépészeti feladatok túlnyomó többségében használható.
De mi miből adódik? Az alap erőket (f) mi definiáljuk a peremfeltételekkel. Merevséget (K) a geometriából és az anyagtulajdonságokból számol a rendszer, de nem elhanyagolható a kontaktok és megfogások hatása sem amit szintén ez a mátrix tartalmaz. Ebből az is következik, hogyrossz peremfeltételekkel a rendszer merevségét akár lényegesen alul, vagy felül tudjuk lőni. Ehhez kapcsolódik a nemlineáris alkalmazása is, hiszen a nemlineáris anyagtulajdonságok, nagy elmozdulások, kialakuló vagy megszűnő kontaktok befolyásolják a rendszer merevségét. Ha ilyen futtatást szeretnénk, ez az egyenleten annyit változtat, hogy a K, illetve az f nem konstans a számítás során, hanem az elmozdulás függvénye.
Szintén fontos információ, hogy a tévhittel ellentétben a megoldó elsősorban nem a feszültséget számolja, hanem az elmozdulást, és abból származtatja a többi eredményt. Ezt felhasználjuk az eredmények kiértékelésekor is. Az egyik alapszabályunk lesz, hogy először nem a számokat, hanem a jelleget vizsgáljuk.
Sok mindennel megismerkedtünk az elképzeléseinket megoldhatóvá tudjuk tenni a számítógépnek és némi betekintést nyertünk a megoldó működésébe is. Ám az igazi munka fele még hátra van, hiszen az eredményeket ki is kell értékelnünk, ami a munka egyik legizgalmasabb része és nem bízhatjuk a számítógépre.
Ezt egy webinár keretében fogjuk átbeszélni.
Tartsatok velünk!
írta: Turcsányi Patrik

