A szimuláció hasznosságáról már többször hallhattatok. Cikkeink közt találtok esettanulmányt és különböző érdekes vizsgálatokat is. Most rendhagyó módon egy cikksorozatban nézzük végig milyen lépések és módszerek javasoltak egy szimuláció és háló építése során. Majd végül megnézzük, hogy tudjuk kiértékelni az eredményeket.
A sorozat folyamán egy kitalált példán keresztül fogunk találkozni olyan problémákkal, amelyek a gyakorlatban is sűrűn előfordulnak. Az első részben most vizsgáljuk meg, milyen előkészületeket érdemes elvégezni valamint, hogy álljunk neki a modell elkészítésének.
Érdemes a feladat elvégzése helyett, ahol a végeredmény a fontos, úgy tekinteni a szimuláció elkészítésére, mint egy folyamatra, ahol megismerjük a szerkezet működését, majd végül eljutunk a kívánt eredményhez. Ahogy egy tervezési folyamatnál vannak különböző revíziók, itt is érdemes különböző megközelítéseket alkalmazni, tesztelni és elemezni a hatásukat.
Ez a gyakorlatban úgy jelenik meg, hogy az egyszerűbb modellel és fizikával kezdünk el haladni a bonyolultabb felé. Ezzel máris kulcskérdéshez érkeztünk, mivel el kell döntenünk, mit szeretnénk, illetve mit érdemes figyelembe venni a vizsgálat során. Erre csak úgy kaphatunk választ, ha fokozatosan lépésről lépésre haladunk az egyre részletesebb kidolgozások fele.
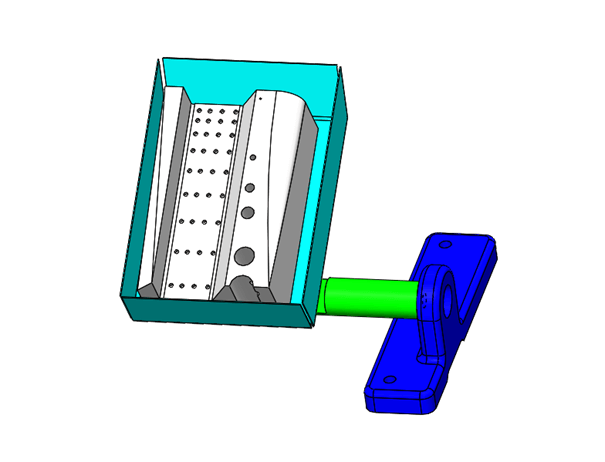
Nézzük is a példánkat, amely így néz ki:

A hozzátartozó feladat, hogy vizsgáljuk meg vajon megfelelő a keretre csavarozott sötétkék műanyag tartó és a hozzá csatlakozó alkatrészek. Feladatuk, hogy megtartsák a dobozt és a benne tartandó ellenőrző készüléket. Láthatjuk, hogy a keret méretéhez képest a szerkezet többi része jelentősen kisebb beleértve a vizsgálandó elemeket is. Továbbá a tartó anyaga műanyag, így a merevsége is jóval kisebb, mint a fém vázé, amelyhez csatlakozik.
Felmerül a kérdés, hogy vajon érdemes-e figyelembe venni az acél szerkezet deformációját? Mennyit veszíthetünk ezzel pontosságban? Az igény egyelőre nem több mint megvizsgálni, hogy elbírja e a tartó szerkezet a készüléket, tehát a súlyát mely kb. 2,5 kg.
A karnyi vastagságú zártszelvényt ekkora terhelés nem fogja megviselni, így az eredményre sem lesz érzékelhető befolyása. Egyszerűsítsük vele a modellt:
ModellKÉSZÍTÉS SZIMULÁCIÓHOZ
Amit kapunk az máris egy átláthatóbb, kisebb méretű modell. Ezt hálózni is könnyebb és gyorsabb, plusz ezáltal a futtatási időn is tudunk spórolni. Megállhatunk-e itt vagy esetleg érdemes további egyszerűsítést végezni? Ha megpróbáljuk behálózni a testet erre sokszor választ kapunk. Itt enélkül is látszik, hogy érdemes még néhány alkatrészt kivenni a számításból, vagy más módon figyelembe venni. De nézzük meg, hogyan láthatjuk a hálózásból min érdemes változtatni.
Közepes hálófelbontással alapértelmezett hálózási módszert használva az alábbi eredményt kapjuk:
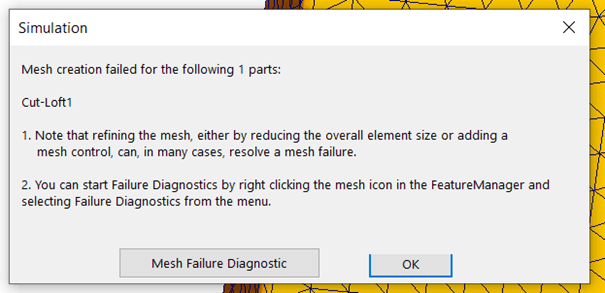
Nem kell csüggedni, ez is eredmény, melyből információt nyerhetünk. Érdekes módon a készülékhez tartozó művelet fut hibára, és nem is hálózza be a testet. Mint ahogy az üzenet is írja ennek számos oka lehet. Próbálkozzunk egy másik hálótípussal. Itt az eredményünk már összetettebb:
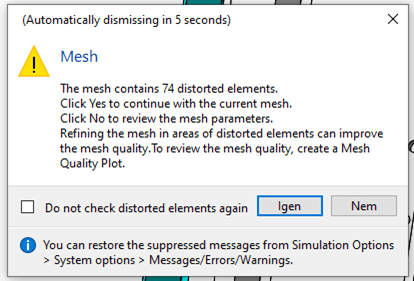
Ez a modellen is látszik:

Látható, hogy a furatok nem lettek jól lekövetve amit egyrészről okozhat a túl durva háló. Ilyenkor két irányba indulhatunk. Az egyik, hogy a háló finomításával próbáljuk megszüntetni a minőségi problémákat. Vagy egyszerűsítjük a modellt. Mivel a furatok kicsik, el lehet tüntetni őket akár egy konfigurációban, vagy akár az egész testet eltüntethetjük. Gondoljunk bele, hogy vajon ez a tömör fém mennyit deformálódik a saját súlya alatt? Gyakorlatilag semmit.
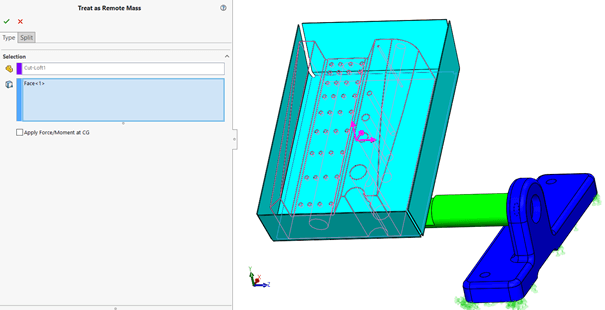
Viszont, ha eltüntetjük mint a vázat akkor, hogy lesz akkor figyelembe véve a tömege?! Erre van speciális eszközünk, tömegpontként fogjuk kezelni:
megtérülő Valóság modellezés szimuláció segítségével
Így behálóznunk nem szükséges, de a tömege hatni fog a kiválasztott felületre. Ezzel szintén kezelhetőbbé tettük a feladatot, így a mi munkánk is kevesebb lesz, illetve a gép is gyorsabban fog számolni.
Eddig a modell előkészítés alapjaival foglalkoztunk, és kicsit beletekintettünk a hálózásba. Belátható, hogy nem érdemes mindent figyelembe venni és az ésszerű egyszerűsítések hamar megtérülnek.
A következő részben megnézzük milyen is egy jó háló továbbá a peremfeltételek megadásával fogunk foglalkozni. Avagy hogyan modellezzük a valóságot.
Tartsatok velünk!
írta: Turcsányi Patrik
